日常で数学の話は<全く>しないので、ブログには書いてみる。笑
バナッハ・タルスキーの定理
タイトルの通り、
Q.「半径1の球」を分解して、再び組み立てて「半径2の球」を作れるか?(´・ω・`)
と問われたら、何と答えるだろうか?
「何馬鹿なこと言ってんの?できる訳ないでしょ?」と言われると思うが、
実は以下のような数学の定理がある。
(厳密性はおいておいて、すごく簡単に書いてみた)
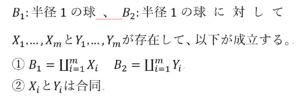
数学嫌いで拒否反応が起こりそうな人のために、要するに文章で言うと、
「半径1の球をm個に分解する。半径2の球もm個に分解する。
そしてそれぞれ分解したm個が、それぞれ全部合同になっている」
という話。
これはつまり
「半径1の球」を分解して、再び組み立てて「半径2の球」を作れる
ということを意味している。
もっと極端にするなら
「サッカーボールを分解して、再び組み立てて、地球にできる」
ということを意味している。
これは「バナッハタルスキーの定理」と言って、数学的にも証明されている定理だ。
興味ある方はネットで調べてもらえればすぐに出てくる。
どういうこと??
もちろん実際問題としてそんなことは不可能だ。( ゚Д゚)
しかしこの定理自体は数学的に正しい。(´・ω・`)
どこが問題なのかというと、
「半径1の球をm個に分解した一個一個の成分X1,…,Xm」たちだ。
m個という有限な個数だが、実際
「X1,…,Xmたちには体積を定義できない」
ということ。
つまり体積を定義できるようなかたちで、半径1の球をうまく分解して、半径2の球にすることはできないということ。
実際にどういう成分になるのかはわからないが、ものすごく変な形になる。
(形というよりは、恐らくすごく稠密なスカスカの集合みたいになる)

考えてみるべき点
この定理から考えてみるべき点はいろいろあるが、その中の一つとしては
「体積」という日常では当たり前の概念も、厳密に定義しようとしたら難しい
ということ。
もちろん日常生活では「全く」困ることはないが、
本当の意味で厳密性を追求しようとすると、簡単な概念ではないし、
曖昧に、適当に「こんな感じっしょ」(‘ω’)ノ と定義してしまうと
このようなパラドックス的なこともたくさん起こってくる。
実は私たちはこういうような「あいまいな定義」をたくさんして生きている。( ˘•ω•˘ )
たとえば「人を殺してはいけない」ということ自体は、
①法律で定められているし
②良心的にもダメそうだから
だめそうだということはわかっている。
しかし厳密に「どうして人を殺してはいけないのか?」と言う問いに対して、「厳密に、完全に」答えられる人が一体何人いるのだろうか?
一番多い回答としては
「私は殺されたくないから、人を殺してはいけないと思う」
というような人が多い。
では
「私は殺されてもいいから、私は人を殺す」
という人が現れてきたら、一体どうするのか?
どうして人を殺してはいけないのか?
信号無視してはいけないのか?
どうして悪口を言ってはいけないのか?
どうして学校のろうかは走ってはいけないのか?
どうして挨拶しないといけないのか?
こういった日常的に当たり前のことも、
厳密に考えてみると、実はとても難しい問題だ。
<曖昧に>、<なんとなく>定義してしまうと
バナッハタルスキーの定理のような
変なパラドックスを起こしてしまうことになる。
ご注意されたし。




コメント